Historia de las mediciones II: Cavendish y la densidad de la Tierra

Historia de los números

Historia de los números I. El cero, los números romanos y los números indoarábigos

Historia de los números II. Los sumerios, los babilonios y el sistema sexagesimal

Historia de los números III. El sistema de numeración egipcio y los papiros Rhind y Boulaq 18

Historia de los números VI. Mayas, los matemáticos que observaban las estrellas

Historia de los números V. La llegada de los números indoarábigos a occidente

Historia de las mediciones

Historia de las mediciones I. Eratóstenes, el hombre que midió la Tierra

Historia de las mediciones II. Cavendish y la densidad de la Tierra

Historia de las mediciones III. Harrison y el problema de la longitud 

Mirad al cielo. Ahora imaginad algo cayendo desde arriba, por ejemplo una manzana. Ahora mirad más arriba, que vuestros ojos atraviesen la lluvia y lleguen hasta los planetas más cercanos, también al Sol y las estrellas. Y si vuestra mente aún os lo permite, retrocedamos en el tiempo 285 años, viajemos hasta el diez de octubre del 1731. Ese día Henry Cavendish acababa de nacer.

Cavendish fue un físico y químico británico altamente conocido por el experimento que lleva su apellido y que pretendía medir la densidad de la Tierra, aunque se le conoce mucho más por lo que nunca hizo: medir la Constante de Gravitación Universal. Ahora bien, ¿cómo mides la densidad de un planeta en el siglo XVIII? Esa es una buena pregunta. 

La densidad es una magnitud que expresa la relación entre la masa y el volumen de un cuerpo. Por ejemplo, ¿os han hecho alguna vez la pregunta de si pesa más un kilo de plomo que un kilo de paja? La respuesta es que pesan lo mismo, aunque un kilo de paja es mucho mas grande. Diríamos entonces que el plomo es mas denso que la paja, pues la relación entre su masa y su volumen indican que si hubiera el mismo volumen de paja que de plomo, el plomo pesaría más. Tampoco hay que confundir masa con peso. En la Tierra conocemos al peso como la fuerza con que la Tierra atrae a un cuerpo, pero nuestro peso sería diferente en Marte o en la Luna. La masa se define como la cantidad de materia que tiene un cuerpo, y sería la misma en cualquier parte del universo. Ahora bien, ¿qué necesitamos para saber la densidad de un cuerpo? La masa y el volumen.

Algunos datos previos

Calcular la densidad de la Tierra requiere dos datos: su volumen y su masa. Si estás pensando que medir el volumen de la Tierra es complicado, tal vez te llevarías una sorpresa al descubrir que, en realidad, es un cálculo muy sencillo que podrías hacer en tu casa con un palo y un metro. Bueno, así es como lo hizo Eratóstenes en el siglo III antes de Cristo, y así es como lo contamos en la anterior entrega de Historia de las mediciones [1].

Ahora bien, ¿cómo medir la masa de la Tierra? Nuestro planeta está compuesto por multitud de materiales diferentes, así que calcular su masa iba a ser muy complicado. Pero ahora es cuando entra en juego un aparato que iba a dar dolor de cabeza a mucha gente: la balanza de torsión.

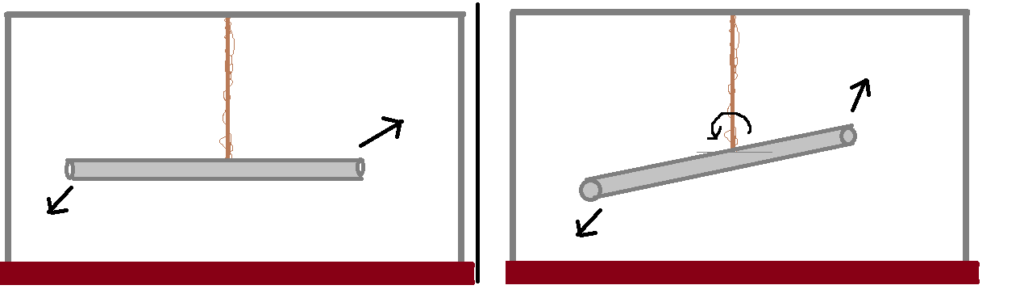
Una balanza de torsión —también llamada por algunos como péndulo de torsión— es un aparato que sirve para medir fuerzas muy débiles, y fue inventada por Charles-Augustin de Coulomb. De hecho, este científico la gastó para medir la fuerza electrostática entre cargas eléctricas, pero ¿en qué consiste una balanza de torsión? Pues básicamente en una barra suspendida por una fibra delgada. La fibra, en este caso, actúa como un muelle de torsión muy débil: por poner un ejemplo, es como si ataras una barra de hierro a un alambre en el centro, y tú te engancharas como un mono de cada uno de sus lados. Si se aplica una fuerza en los extremos de la barra, esta girará hasta que alcance un equilibrio donde la fuerza de torsión del alambre sea igual a la fuerza aplicada, y la barra se detendrá. De hecho, si dejaras de aplicar la fuerza, el alambre se desenrollaría y comenzarías a dar vueltas en la otra dirección. La gran sensibilidad se obtiene gracias a que una fuerza muy débil puede causar una rotación muy grande.

Figura 1: Ejemplo básico de funcionamiento simplificado de una balanza de torsión

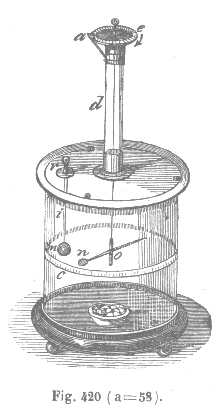
Ahora bien, ¿qué es lo que hizo Coulomb? Su balanza era una barra aislante con una bola revestida de metal en el extremo, y además estaba suspendida por un hilo de seda. Y ¿qué se hacía con esa bola? Se cargada con electricidad estática con carga positiva, y a su vez una segunda bola cercana a la primera era cargada también con cargas positivas, y como cargas iguales se repelen, la barra giraba, se torcía la fibra un cierto ángulo, que a su vez se podía medir fácilmente. De ese modo podía calcular cuánta fuerza se necesitaba para torcer la fibra, y Coulomb calculó la fuerza que había entre las bolas cargadas. Pero no se quedó ahí, sino que probó diferentes cargas y separaciones, demostrando matemáticamente que había una ley de proporcionalidad inversa-cuadrada, que ahora se llama Ley de Coulomb.

Figura 2: Balanza de torsión utilizada por Coulomb

Vale, pero ¿qué tiene que ver todo esto con Cavendish? Pues que nuestro hombre tuvo una idea, ¿y si se hiciera algo parecido para medir la fuerza con la que se atraen dos bolas metálicas debido a la fuerza de la gravedad? No olvidemos que, según la física clásica, todo cuerpo con masa ejerce una fuerza gravitatoria sobre otro, por lo que dos cuerpos se atraen debido a la gravedad. Y ojo, porque no me refiero solo a la Tierra atrayendo a la manzana de Newton, la Luna o a los satélites de comunicaciones que orbitan nuestro planeta, sino también, ¿por qué no?, a la atracción entre dos manzanas. Y es que, aunque no sintamos esa fuerza, las dos frutas se estarían atrayendo. Pero claro, esa fuerza de atracción gravitatoria es mucho menos intensa que las fuerzas que intentaba medir Coulomb, y se requería para ello una balanza mucho más grande y compleja. Y Cavendish la construyó.

La balanza de torsión de Cavendish

Si bien Coulomb impulsó el concepto de balanza de torsión, otros científicos pensaron en darle algún uso en el estudio de la fuerza de la gravedad. De hecho, el primero en proponer el experimento no fue Cavendish, sino John Michell. Pero ¿quién fue ese hombre? Michell nació en 1724, y entre otras cosas fue el primero en elucubrar el concepto equivalente a un agujero negro en la física newtoniana; lo que él llamó una estrella oscura. El planteamiento era el siguiente: una estrella tan densa que ni siquiera la luz podía escapar de ella. De hecho, Michell hizo una serie de cálculos que le permitieron afirmar que una estrella con un diámetro 500 veces más grande que el del Sol, atraería a la luz de forma tan fuerte que no podría escapar, dando por resultado una estrella invisible. Ahora bien, esto es apasionante pero el motivo de traer a Michell a este artículo es porque diseñó un experimento con una balanza de torsión para medir la densidad de la Tierra, pero lamentablemente murió antes de poder terminar su aparato. Su balanza, a mitad construir, fue heredada por un miembro de la Royal Society, Francis J. Hyde, que después la regaló a Henry Cavendish.

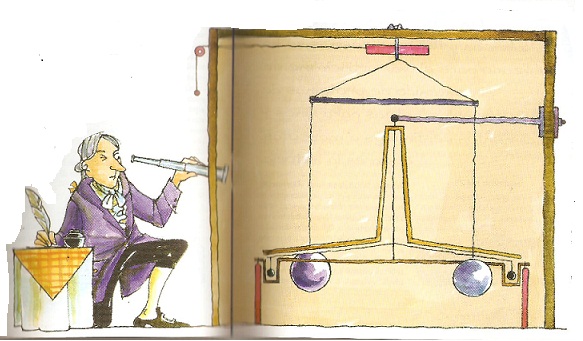
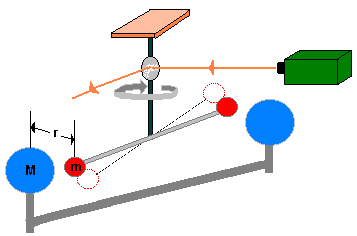
Cavendish tenía media balanza pero no estaba contento. Si bien el aparato ideado por Michell era interesante, consideró que era insuficiente para obtener una medida adecuada y lo desmontó para reconstruirlo a su gusto. Finalmente, su balanza de torsión consistió en un palo horizontal de unos dos metros de alto, y en cuyos extremos había dos esferas de plomo de idéntica masa. El palo estaba colgado de un hilo, siguiendo el esquema básico de una balanza de torsión. Y lo interesante vino a continuación: cerca de las dos esferas, nuestro físico colocó otras dos esferas de 175 kg de peso cada una, esperando que su masa atrajera a las bolas de menor peso gracias a la gravedad. Además, para evitar que el aire u otras masas cercanas distorsionaran el experimento, todo se hizo en una habitación cerrada y observándolo a través de un telescopio.

Figura 3: Reconstrucción del experimento

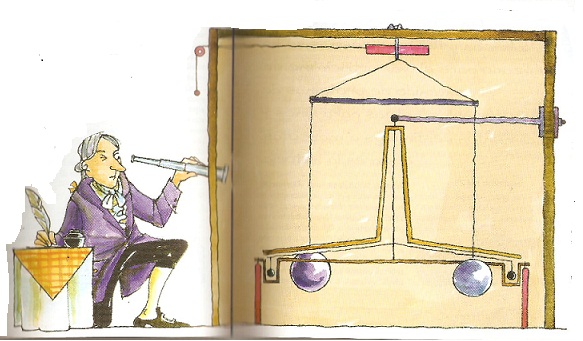
Básicamente, lo que hizo Cavendish puede resumirse así: cuando las dos esferas grandes estaban cerca de las pequeñas, estas eran atraídas y hacían que la barra girara, por lo que en ese punto se daba una situación de equilibrio donde la fuerza de torsión era igual a la fuerza gravitatoria entre los dos cuerpos. El ángulo producido se medía gracias a la desviación en un rayo de luz (linea naranja de la siguiente ilustración) que se producía al situar un pequeño espejo al que le llegaba un haz luminoso. Y finalmente Cavendish tuvo todos los datos para calcular la masa de la Tierra.

Figura 4: Funcionamiento de la balanza de torsión de Cavendish

Sin entrar en muchos cálculos, los cuales podéis consultar en el artículo de las referencias [2],  Cavendish calculó la atracción entre las bolas a partir del período de oscilación, y a partir de ese dato calculó la densidad de la Tierra gracias a extrapolar los datos de sus bolas al caso de nuestro planeta. Pero ¿cual fue el resultado? El cálculo que obtuvo fue que la densidad de la Tierra es, en su promedio, 5,48 veces superior a la del agua, aunque después de la publicación otro investigador se dio cuenta de que Cavendish había cometido un pequeño error de aritmética: el cálculo real con los datos de la medición debería haber sido de 5.448 veces la densidad del agua.

El valor de la constante universal G

La constante de gravitación universal (G) determina la intensidad de la fuerza de atracción gravitatoria entre los cuerpos, y es una constante fundamental tanto para la Ley de gravitación universal de Newton como para la Teoría general de la relatividad de Einstein. Ahora bien, antes dije que Cavendish es conocido por lo que nunca hizo: calcular el valor de la constante universal G, pero entonces, si no lo calculó, ¿por qué mucha gente cree que lo hizo? Porque para el cálculo de dicha constante hacía falta tener tres números: el valor de la gravedad terrestre calculado por Newton, el valor del radio terrestre calculado por Eratóstenes y explicado en el primer artículo de esta saga, y finalmente el valor de la masa terrestre, que fue el último de los valores encontrados gracias a Cavendish. Con esos tres números podemos calcular la Constante Gravitatoria Universal G, pero Cavendish no lo hizo. Es más, ni siquiera se menciona G en su artículo.

Tal vez os estéis preguntando por qué Cavendish, teniendo todos los elementos, no hizo el cálculo y se anotó ese punto en su marcador. La respuesta es que en 1798, cuando Cavendish publicó sus resultados, la distinción moderna entre peso y fuerza no se había realizado. El sistema métrico acababa de ser inventado pero no se utilizaba en el mundo anglosajón, por lo que tanto la masa y la fuerza se medían en libras. Y esto nos lleva a que la constante G no se definió hasta 1894, a pesar de que su existencia estaba implícita en los cálculos de Cavendish. De hecho, actualmente sigue el debate sobre si Cavendish determinó realmente el valor de G o solamente la densidad de la Tierra.

Dejando eso aparte, ¿cual fue la importancia del cálculo de G? Si bien en la Tierra podemos pasear una mañana de primavera por el campo y dejar caer una manzana para medir el famoso 9.8 m/s², es decir, la gravedad terrestre calculada por Newton, es un poco más difícil de realizar eso mismo en Venus, Saturno, o en el mismísimo Sol, así que no se podía calcular la masa de ningún otro cuerpo del Sistema Solar. Pero gracias al cálculo de G, la famosa ley de gravitación universal de Newton pudo usarse por fin de manera muy útil.

Ley de gravitación universal de Newton

Desde que se supo el valor de G, gracias a la tercera ley de Kepler y conociendo la duración del año terrestre, la distancia de la Tierra al Sol y la constante gravitacional (G), se podía calcular la masa solar. Y la buena noticia era que, gracias a las mediciones del tránsito de Venus realizadas en 1769 —es decir, 29 años antes de la publicación de Cavendish— ya se conocía la distancia del Sol a la Tierra. Esto nos lleva a que el cálculo de Cavendish no solo sirvió para medir la masa de nuestro planeta, sino también la del Sol y, a partir de ese dato, también la del resto de planetas; y todo ello gracias a un hombre que con unas bolas de metal, unas cuerdas y unos palos, se propuso medir el universo desde su casa.

La medida de la masa del Sol tuvo un resultado paradójico: en la época de Cavendish no se conocía la energía termonuclear, así que se pensaba que el Sol emitía energía gracias a una combustión ordinaria. Suponiendo que el Sol estuviera hecho de carbón en combustión —no tenían otras alternativas para explicar por qué emitía calor y luz— la masa del Sol arrojaba un resultado desconcertante: calculando cuánto tiempo podía arder una bola de carbón de su masa, la respuesta era más cercana a la edad bíblica de la Tierra que a la edad geológica real, y ese fue uno de los argumentos científicos más importantes en contra de la teoría de la Tierra antigua que se necesitó, entre otras cosas, para explicar cómo la evolución por selección natural había creado formas de vida complejas gracias a un proceso tan lento.

Y, ¿qué nos deja toda esta historia como lección final? Que incluso las cosas más grandes pueden intentar ser medidas con métodos que requieren materiales ordinarios, y sí Eratóstenes y Cavendish fueron capaces de medir la Tierra y calcular la densidad del Sistema Solar utilizando poco más que palos, cuerdas y esferas de metal, en la era de la exploración espacial se abre todo un horizonte de posibilidades que tendremos que abordar con ingenio, pasión, y sin los limites cognitivos que hemos recibido como herencia evolutiva. Sobre Cavendish, por si lo que hemos contado aquí fuera poco, como químico descubrió el hidrógeno y la composición del agua. Así que cuando bebemos agua o miramos las estrellas, de algún modo Cavendish está ahí, mirándonos a través de 285 años de historia.

Referencias

[1] Historia de las mediciones I: Eratóstenes, el hombre que midió la Tierra

[2] Artículo de los cálculos de Cavendish