El nacimiento de una nueva Física, parte IV: La física cuántica

Texto escrito por Víctor Buendía Ruiz-Azuaga

Y aquí está, ya hemos llegado. Tras tres artículos, y unos 40 años de problemas sin resolver, vamos a ver cómo nació finalmente lo que hoy conocemos como física cuántica, la disciplina de la física que estudia las propiedades de los sistemas microscópicos.

Como siempre, comenzaremos con una recapitulación: hemos encontrado diversos fenómenos que no podemos explicar con la ciencia conocida hasta el momento. La solución se ha ido poniendo a parches. Comenzamos por decir que la energía no se intercambiaba de forma continua; luego, llegamos a ser más atrevidos y decir que la energía no es un continuo. Y aunque esto resolvió cuestiones importantes, aún tuvimos que abandonar nuestra intuición y pensar en ondas y partículas materiales como una sola cosa. Los éxitos de estas soluciones son notorios: con esto se explica el efecto fotoeléctrico, el experimento de la doble rendija, y creamos un nuevo modelo atómico mucho más completo, incluso coherente con los espectros atómicos.

Sin embargo, los propios científicos de la época son conscientes de que esto no son más que parches. Han aplicado algunas ideas que funcionan, pero no saben claramente por qué o si realmente estas son verdad. El siguiente paso es encontrar un marco teórico capaz de aglutinar todos estos parches en una única teoría.

La mecánica matricial

La mecánica matricial es la primera explicación completa que se le da a estos parches. El primer artículo sobre el tema se publica por Heisenberg en 1925. La idea de Heisenberg en sencilla en teoría: el problema principal es que trabajamos con “partículas” como electrones, de los cuales no podemos conocer ni su posición ni su velocidad de forma directa; en su lugar, podemos medir frecuencias de onda e intensidades. De modo que lo que hacemos es simplemente unas transformaciones en las ecuaciones, para eliminar la posición, velocidad y otros parámetros clásicos y sustituirlos por los que podemos observar en el laboratorio.

El resultado fue un poco desconcertante para la gente que trabajaba con Heisenberg, porque al final del desarrollo, lo que aparecía eran matrices, unos elementos matemáticos que, para hacernos una idea, son “tablas” de números, sobre las que podemos definir varias operaciones. Hoy día cualquier ingeniero o físico sabe trabajar con matrices, pero en esta época solamente los matemáticos las habían estudiado. El matemático Jordan fue quien se dió cuenta de que en realidad estos resultados eran matrices y ayudó al equipo de Heisenberg a hacer sus cálculos más sencillos. Aún así, la mecánica matricial resultaba bastante complicada dado que empleaba un formalismo matemático desconocido para los físicos.

Por otro lado, el matemático Dirac, también muy implicado con la teoría cuántica, consigue estos mismos resultados a partir de otro concepto diferente. Mediante una sólida teoría matemática Dirac obtiene los mismos resultados que Heisenberg y compañía, pero curiosamente no se da cuenta.

Esta teoría es aplicada para modelizar con más precisión, por ejemplo, el átomo de Hidrógeno, con unos resultados excelentes. No solo era capaz de reproducir por completo el modelo de Bohr, sino que además, explicaba más desdoblamientos de líneas espectrales.

Pero cuando este grupo alemán de físicos pensaban haber encontrado la panacea, aparece otra teoría capaz de hacer lo mismo que la suya: la mecánica ondulatoria.

La mecánica ondulatoria

Esta es otra forma de ver la física cuántica, también capaz de aglutinar todos los parches y reproducir exactamente los mismos resultados que la mecánica matricial. Fue introducida por Schrödinger en 1926.

Schrödinger parte, al igual que Dirac, de las ecuaciones de la mecánica clásica para justificar su teoría. Sin embargo, Dirac emplea álgebra, mientras que Schrödinger utiliza un punto de vista del cálculo variacional. Este nuevo enfoque matemático le llevará finalmente a la famosa ecuación de Schröndinger; vale la pena resaltar que, aunque Schrödinger justifica su fórmula a partir de la física clásica, hoy día esta ecuación se admite como un postulado, es decir, sin demostración, es cierta porque sí (y porque funciona). Y esta ecuación seguirá siendo fundamental mientras siga dando resultados experimentales tan buenos como hasta ahora.

El caso es que esta ecuación nos dice cómo evoluciona un sistema cuántico en el tiempo, y su resolución nos lleva a las mismas soluciones que la mecánica matricial; la diferencia es que la mecánica matricial se basa más en la idea del corpúsculo, del electrón, visto mediante las variables que observamos en el laboratorio, en lugar de las habituales, mientras que la mecánica de Schrödinger se basa en la idea de que el sistema se comporta como una onda; eso sí, no podía decir qué era realmente lo que vibraba en esta onda.

Este formalismo se hizo mucho más popular, a pesar de ser posterior. ¿Por qué, si era equivalente al que ya había? Sencillamente, porque todos los físicos manejas estupendamente las ondas, pero en aquella época pocos sabían emplear las matrices. De hecho, este método era tan sencillo conceptualmente que incluso los creadores de la mecánica matricial pasaron a emplear este para algunos problemas concretos.

Poco después, Von Neumann demostraría que ambas formas de ver la Mecánica Cuántica eran completamente equivalentes; actualmente la teoría empleada es la propuesta por Von Neumann, que unía las dos anteriores, mediante el formalismo matemático creado por David Hilbert.

Curiosamente, Hilbert se divirtió bastante con toda esta situación. Heisenberg y Born fueron a pedirle ayuda para resolver problemas matemáticos con las matrices. Tras echarle una ojeada, dijo que él había estado estudiando ese tema últimamente, y recomendó, en lugar de usar las matrices, buscar una ecuación diferencial equivalente. Born y Heisenberg pensaron que el planteamiento de Hilbert no era bueno, y decidieron no hacerlo. Si lo hubieran hecho, habrían obtenido la ecuación de Schrödinger y toda la mecánica ondulatoria. No lo hicieron, y fue el austríaco quien se adelantó y puso su nombre a la ecuación. Sobre esta situación, Born comentó que nunca se perdonaría el error de no haber hecho caso a Hilbert.

Las consecuencias

Ahora ya conocemos las herramientas, y vamos a hablar un poco de los primeros resultados a los que llevó esta teoría.

Una de las primeras interpretaciones fue la misteriosa onda propuesta por Schrödinger. ¿Qué es lo que vibraba en la onda? La idea que usamos actualmente es la interpretación de Born, que nos dice que esta onda tiene una interpretación de probabilidad. Es decir, representa la probabilidad de encontrar a la partícula en cierto estado. Cuando se mide una única partícula, no se sabe qué resultado se va a obtener. Hay que medir una cierta cantidad, por ejemplo un millón de partículas, y el resultado será que un 70% cumple tal, un 20% tal otra cosa y el otra 10% restante. Estos números son los que da la física cuántica, las probabilidades de obtener los resultados, y por supuesto, cuáles son estos resultados. Aunque parezca extraño, funciona con una precisión tremenda.

Otra consecuencia es el principio de incertidumbre de Heisenberg. Durante sus investigaciones, Heisenberg observó que aparecía una desigualdad que impedía medir velocidad y posición simultáneamente con precisión infinita. Es decir, normalmente, si yo tengo una partícula, en física clásica puedo ver dónde está y a qué velocidad se mueve (como en una especie de radar). Si mi radar es infinitamente bueno, podré saber con exactitud cómo se mueve la partícula. Pero en física cuántica esto no ocurre; en mi radar puedo ver perfectamente dónde se encuentra la partícula, pero no cómo de rápido se mueve. E igualmente, puedo saber su velocidad, pero a cambio de conocer dónde está. También puedo medir ambas simultáneamente, pero en ese caso tendré cierto error experimental, es decir, como si mi radar no fuera infinitamente bueno. Y esto no hay manera de arreglarlo. El principio de incertidumbre luego se generalizó no solo para posición y velocidad, sino para otras magnitudes. Hay que destacar que no a todo par de magnitudes le ocurre esto, pero sí hay muchas sometidas al principio de incertidumbre.

Todo esto de la probabilidad lleva a eliminar por completo algunos conceptos clásicos. Por ejemplo, en mecánica cuántica no podemos hablar de trayectoria. La trayectoria de una partícula no existe, en absoluto. La partícula no tiene posición cuando no la medimos, y tras la medida, no podemos decir dónde está. Sé que cuando medí estaba ahí. Antes o después, no se sabe. Y lo que es aún peor, la partícula, por ejemplo el electrón, mejor pensar que ni existe cuando no la miras. Einstein siempre fue contrario a la idea de que la probabilidad fuera totalmente inherente a la teoría, que llevaban a consecuencias como ésta. Él, junto otros físicos de mente más tradicional pensaban que había alguna solución a la mecánica cuántica, otro formalismo matemático distinto en el cual pudieran olvidarse de todas estas probabilidades, en el que hubiera una realidad en el sistema, y no un montón de variables aleatorias. El caso es que estas ideas tan estrambóticas se fueron comprobando experimentalmente, de forma que al final tuvo que admitir el éxito de esta nueva teoría, aunque no quedara muy convencido.

Más consecuencias divertidas, por ejemplo, el efecto túnel. Es una consecuencia que aparece matemáticamente de forma natural al estudiar la ecuación de Schrödinger; supongamos que existe lo que se llama una barrera de potencial. Básicamente, esto es simplemente hacer alguna fuerza sobre la partícula, y puede ser vista como una especie de pared (o un escudo de fuerza, para los amantes de la ciencia ficción). Realmente, el concepto de barrera de potencial representa situaciones como un electrón en un campo electromagnético, una pelota rebotando entre dos paredes, o un cuerpo atrapado por la gravedad de un planeta. Por ejemplo en el dibujo siguiente aparece una partícula clásica encerrada en un pozo de potencial.

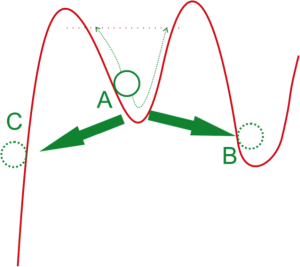
Si esta partícula tiene cierta energía, puede moverse oscilando. Si le damos la suficiente, aumentando su velocidad, incluso puede salir del pozo y bien iniciar una trayectoria hacia abajo o caer encerrada en otra parte del potencial. En principio, la partícula, si no tiene suficiente energía, no puede escapar de nuestra barrera. Sin embargo, en física cuántica, si el grosor de la pared no es demasiado, puede directamente atravesarlo. Es decir, nuestro electrón puede salirse del campo electromagnético, o la pelota atravesar una de las paredes. El motivo de este puede ser visto por el principio de incertidumbre. Supongamos que tenemos una partícula cerca de una pared, y que medimos su posición de forma exacta. Entonces sabemos a qué lado está de la pared, pero no conocemos su velocidad. Podría entonces llevar suficiente velocidad como para atravesar la barrera. Por otro lado, si mides su velocidad y te aseguras de que no tienen suficiente como para pasar, da igual, porque entonces no conocemos la posición. La partícula podría estar a cualquier lado de pared. ¿Que cómo ha llegado ahí? Pues porque tiene probabilidad de llegar. Si toca, pues toca y la atraviesa. Este extraño efecto tiene diversas aplicaciones en electrónica, por ejemplo, ¿sabías que el pendrive borra la información contenida en él empleando efecto túnel?

Por último, el parche: ¿de dónde aparecen los cuantos, los paquetitos de luz de los que llevamos hablando tres entradas? ¿Dónde ha quedado eso? Cuando se resuelve la ecuación de Schrödinger para una partícula que está atrapada en una barrera de potencial, la ecuación que aparece tiene varias soluciones, separadas entre sí. Mientras que en física clásica obtienes valores continuos para la energía, en física cuántica las ecuaciones siempre llevan a que solo ciertas energías, múltiplo de una, son posibles. Estos resultados coinciden con todos los obtenidos en los años anteriores, y añade por fin una explicación teórica a lo que hemos tratado de explicar en los últimos artículos.

Aunque podría seguir durante un buen rato hablando de consecuencias de la física cuántica, lo voy a dejar aquí, por ahora. Hay muchísimas cosas más y espero que en un futuro dedique algún artículo a describir algunos experimentos como los de Bell, o los de entrelazamiento cuántico, que son más complicados de entender, y de vital importancia, y necesitan más espacio del que pueda dedicarles aquí. En todo caso, se ha avanzado mucho en física cuántica, y se ha convertido en uno de los mayores éxitos de la física. A pesar de su carácter aleatorio y probabilístico, es una de las ramas de la ciencia donde se obtiene resultados experimentales más de acuerdo con los teóricos. Aún quedan algunos problemas que solventar, y esperamos ver aún nuevas ideas geniales y extrañas en una teoría de la gravedad cuántica.

Por mi parte, espero que hayáis disfrutado de la serie de artículos y conozcáis, aunque sea de forma resumida, cómo se abre una disciplina de la ciencia progresivamente. ¡Los comentarios son ahora vuestros!

Víctor Buendía Ruiz-Azuaga