Texto escrito por Víctor Buendía Ruiz-Azuaga
En este texto vamos a comentar la estrecha relación que une a la física y a la música. Tanto para aquellos que sepan música y no sepan mucha física, como para los que sepan algo de física y no sepan nada de música. El tratamiento va a ser histórico, desde la teoría fundamental griega hasta una idea más actual (que no completa) del sonido. No se pretende realizar un análisis completo y detallado, pero espero que sirva de resumen fundamental para todas aquellas personas que quieran conocer un poco más de los ambos mundos.
Lo primero es conocer un par de conceptos que se utilizan en música habitualmente y que mencionaremos mucho en lo que sigue:
- Un intervalo es, en música, la distancia que hay entre dos notas. Los intervalos pueden ser de 2ª, 3ª, 4ª, etc. Para calcular el intervalo entre dos notas, simplemente contamos las que hay entre ellas: Entre Do y Fa hay una 4ª porque contamos Do, Re, Mi, Fa. Cuatro notas.
- Los intervalos se pueden dividir en subcategorías dependiendo del número de tonos y semitonos entre las dos notas. De todas formas, no voy a explicar la clasificación completa de los intervalos ahora porque es algo larga y no la necesitamos para nuestro análisis.
- Cada nota puede tocarse en distintas octavas, es decir, se puede tocar “Do grave” o “Do agudo” y así con muchos Do diferentes. Para evitar confusiones, se llama La 4 al La que se utiliza para afinar. El “La agudo” sería La 5 y un La aún más agudo, La 6, etc. Por debajo tendríamos La 3, La 2…
- Hay que hacer notar que lo que un músico entiende por altura de una nota es lo que un físico llama la frecuencia de la onda. Una frecuencia más alta quiere decir un sonido más agudo, y una frecuencia más baja, uno más grave. La frecuencia se mide en Hertzios (Hz), y la frecuencia de la nota del La 4 es de 440 Hz.
La música en la Antigua Grecia: el monocordio.
Se sabe que los griegos poseían un sistema musical bastante desarrollado, que les permitía escribir partituras utilizando una notación alfabética, es decir, representaban cada nota mediante una letra. Pero aparte de la práctica musical, se conoce fundamentalmente la música griega por la gran cantidad de artículos teóricos que conservamos de ella.
No nos vamos a centrar ahora en la teoría musical griega, que es bien extensa; vamos a hablar, fundamentalmente, del monocordio, que es una de las piezas clave que unen a la física con la música. El monocordio, como su nombre indica, es un instrumento formado por una única cuerda, tensada y sujeta por sus dos extremos. El interés del monocordio es que, mediante una pieza deslizante, se puede “acortar” la longitud efectiva de la cuerda para cambiar el sonido que esta produce.
Pues bien, los griegos se dieron cuenta de que al acortar la longitud de la cuerda a la mitad, el sonido era esencialmente el mismo, pero más agudo: este es el sonido de octava. Si la cuerda tocaba un La 4, entonces al poner la pieza a la mitad el nuevo sonido era un La 5. Los nombres de las notas no eran iguales para los griegos, pero ambos sonidos les sonaban bien, y la 8ª fue un intervalo importante para ellos. Algo parecido ocurrió con cuando la pieza se colocaba a 2/3 del extremo. Este sonido, es un intervalo de 5ª, además, de la llamada 5ª Justa. Si la nota que tocaba la cuerda era La 4, la nota que sonaba entonces era Mi 5. (Porque subimos cinco notas, La 4, Si 4, Do 5, Re 5, Mi 5).
A los griegos les gustaban estos intervalos, y siguieron usándose fundamentalmente durante mucho tiempo, hasta el final del canto gregoriano en el siglo XV (sin hacer caso a intervalos de 3ª y 6ª, que son propios de la música a partir del siglo XVI y que siguen hasta nuestros días). El sistema de afinación pitagórico se basaba en ir afinando las notas de 5ª en 5ª. Sin embargo, poniendo la pieza deslizante en otros lugares de la cuerda, siempre usando fracciones, aparecen el resto de los intervalos: a 8/9, aparece la 2ª; a 3/4, la 4ª y así con todos. ¿Por qué ocurre así?
La respuesta a esta cuestión se encuentra en la física. Con las herramientas que nos proporciona la física de ondas, es fácil calcular cuál es la frecuencia emitida por una cuerda vibrante. Creo realmente interesante incluir aquí la expresión, pues es muy sencilla:
Donde n es un número entero, que puede ser cualquiera (este asunto lo discutiremos más adelante), L es la longitud de nuestra cuerda, r su radio, y ρ su densidad. F es la fuerza con la cual tensamos nuestra cuerda. De la fórmula deducimos lo siguiente:
- Una cuerda más larga, o más gruesa (de mayor radio) produce un sonido más grave.
- Si aumentamos la fuerza de tensión sobre la cuerda, el sonido se hará haciendo lentamente más agudo.
También se puede cambiar la densidad de la cuerda, pero eso usualmente no es sencillo en comparación con el resto de los parámetros. Observemos lo que ocurre cuando hacemos como los griegos, y reducimos la longitud de la cuerda a la mitad. En ese caso, si el lector sabe algo de matemáticas, puede ver rápidamente que al escribir L/2 en el lugar de L, nos queda la expresión equivalente a 2f. Si escribimos 2L/3 en lugar de L, el resultado es 3f/2. Efectivamente, aparecen frecuencias cada vez más agudas, tal como les sucedía a los griegos. Entonces, nos surge la siguiente idea genial: sabemos que, al tocar una 5ª (moviendo la pieza hasta 2/3 de la longitud) por ejemplo, La – Mi, la frecuencia aumenta en 3/2, es de decir Mi = 3/2 La. Conocemos la frecuencia de la nota de afinación, La 4, de modo que, utilizando estas fracciones, podemos calcular las frecuencias de todas las notas musicales según el sistema griego. Hagámoslo. ¿Qué ocurre cuando comparamos las frecuencias obtenidas por este método de fracciones con las frecuencias de afinación de un piano actual…?
|
Do 4 |
Re 4 |
Mi 4 |
Fa 4 |
Sol 4 |
La 4 |
Si 4 |
Do 5 |
|
|
Piano |
261.6 |
293.7 |
329.6 |
349.2 |
392.0 |
440.0 |
493.9 |
523.3 |
|
Fracciones |
264.0 |
297.0 |
330.0 |
352.0 |
396.0 |
440.0 |
495.0 |
528.0 |
|
Diferencia |
3.4 |
3.7 |
0.4 |
3.2 |
4.0 |
0.0 |
1.1 |
5.3 |
Vaya, vaya, aquí tenemos algo interesante. Las frecuencias de la fila correspondiente a las frecuencias del piano se pueden encontrar en la bibliografía (por ejemplo en Wikipedia), aunque hay una fórmula exacta que nos da esos mismos valores. La de abajo, se obtiene multiplicando la frecuencia de la columna adyacente por la fracción correspondiente. Por ejemplo, entre el Fa y el Sol hay una relación de 9/8, mientras que entre La y Sol es de 10/9. Así, si La 4 = 440 Hz, entonces Sol 4 = 440 x 9 / 10 = 396 Hz y la siguiente nota es Fa 4 = 396 x 8 / 9 = 352 Hz.
Sistema temperado
El caso es que, en resumidas cuentas, hay diferencias que no parecen seguir ningún patrón. Es más, conforme nos alejamos de La 4 estas diferencias comienzan a aumentar sin control. Esto es porque en el sistema de los griegos, el sistema pitagórico, se basa en una afinación distinta de la actual. Este sistema consigue una consonancia perfecta con los intervalos de 8ª, 4ª y 5ª, pero tiene deficiencias a la hora de afinar la 3ª y 6ª. Cuando estos intervalos comienzan a usarse, pronto los músicos se dan cuenta de que tienen que cambiar su sistema de afinación y abandonar el sistema de fracciones.
En este problema trabajan una buena cantidad de teóricos musicales durante el final de la Edad Media y, especialmente durante el Renacimiento, los intervalos de 3ª y 6ª empiezan a tomar protagonismo. Hay que destacar al español Bartolomé Ramos de Pareja que mejora bastante el sistema de afinación para estos intervalos, aunque no encuentra una solución definitiva.
Finalmente la solución consiste en dividir la octava en doce sonidos iguales. Basta decir “¡entre La 4 y La 5 esto quiero dividirlo en 12 sonidos iguales!” para ver que para obtener la frecuencia de una nota, conocida la anterior, basta multiplicar por la cantidad 
. Podéis comprobar que si vamos multiplicando las frecuencias de la tabla anterior por esta cantidad, se obtienen las demás con buena exactitud. El sistema temperado, a pesar de tener también algunos problemas, es el que se mantiene aún hoy día para afinar la mayoría de los instrumentos. Este sistema fue popularizado por J.S. Bach en su colección de obras para clave (antecesor del piano) “El clave bien temperado”.
Armónicos, cuerdas vibrantes y tubos cerrados
El siguiente paso de nuestro análisis es fijarnos en la cualidad del sonido llamada timbre. Los músicos lo definen simplemente como “la cualidad que caracteriza a los sonidos y permite distinguir unos de otros”, es decir, lo que nos permite diferenciar una flauta, un violín y un piano. Pero, ¿qué hace diferentes a estos sonidos?
La respuesta está en la misteriosa n de la fórmula anterior. Habíamos dicho que puede tomar valores enteros, es decir, 1, 2, 3… pero no habíamos comentado su utilidad. El caso es que una cuerda, tensa y sujeta por sus dos extremos, puede vibrar de varias formas. Según como vibre, producirá una frecuencia distinta, y ése es nuestro parámetro n. En física, a las formas que tiene una cuerda de vibrar se les conoce como modos de vibración.
En nuestro instrumento musical, al tocar una nota, la cuerda no vibra con un solo modo de vibración, sino que se producen varios de forma simultánea. Incluso es posible que nuestro instrumento toque varias cuerdas a la vez para producir más modos de vibración. Por supuesto, el sonido que suena con más fuerza es el fundamental, el que corresponde a nuestra nota, la modo de vibración n=1, pero hay muchos más acompañándolo, que en música denominamos armónicos.
Haré un comentario sobre los instrumentos de viento; éstos se comportan o bien como tubos abiertos, o bien como tubos cerrados. La gracia es que como los tubos se comportan matemáticamente igual que las cuerdas, me basta estudiar cuerdas para saber cómo funcionan los tubos, y viceversa. La diferencia entre los tubos cerrados por los dos lados (o cuerdas sujetas en ambos extremos) y los tubos abiertos por un lado (o cuerda sujeta solo por un extremo) es precisamente en que no tienen los mismos modos de vibración, y por tanto, no tienen los mismos armónicos: los tubos abiertos por un lado solo contienen los modos impares, 2n+1.
Fourier, los espectros y los números imaginarios
Hemos dicho que tenemos unos sonidos, que tienen distintos armónicos, dependiendo del instrumento. Es claro que el timbre va a depender, pues, de estos armónicos, que son los que le van a dar su forma al sonido. Por tanto, para modelar el sonido lo único que necesitaría saber es qué frecuencias contiene y con qué intensidad suena cada una de esas frecuencias. Por supuesto, como siempre, hay más detalles, pero lo fundamental es eso.
La herramienta utilizada actualmente para tratar con el sonido son los números complejos, o imaginarios. Estos no son números “para contar”, es decir, no existen realmente, pero son una herramienta matemática muy útil; una de sus utilidades es para trabajar y operar con ondas. Con ellos, demostrar las fórmulas de los tubos, las cuerdas y otras mucho más complicadas es sencillo, lo que permite estudiar de manera sencilla fenómenos como qué ocurre cuando el sonido cambia de medio o cuando hay interferencias.
Pero otra de las cosas que podemos hacer usando números complejos es la llamada transformada de Fourier. Con esta herramienta matemática, podemos descomponer una función temporal (por ejemplo, la grabación de un violín tocando un La) en una función que depende de las frecuencias, es decir, podemos obtener precisamente los armónicos del sonido y sus intensidades. A esta representación se le denomina espectro del sonido, y es más o menos lo que controlamos cuando tocamos el ecualizador el aparto de música: seleccionamos a qué volumen queremos cada una de las bandas de frecuencias de las canciones. Esto es realmente interesante en edición de sonido. Usando las herramientas de transformadas de Fourier y números complejos, se ha avanzado mucho en la tecnología de la síntesis de sonido y de voz, dando lugar a una gran cantidad de nuevos sonidos con los sintetizadores.
Por último, voy a hacer una gran síntesis de todo lo que he explicado en el artículo con un solo ejemplo.Para comenzar, he cogido la frecuencia Do 4 = 261.63 Hz. Luego, supooniendo unas características de una cuerda de piano, calculo la frecuencia de los primeros modos de vibración de la cuerda cambiando la n.
|
n |
Frecuencia (Hz) |
|
1 |
263.61 |
|
2 |
523.26 |
|
3 |
784.9 |
|
4 |
1046.52 |
|
5 |
1308.15 |
|
6 |
1569.78 |
|
7 |
1831.41 |
Después, he grabado la nota Do 4 en mi piano y he representado su espectro mediante una utilidad informática, y he señalado los numeritos que me dan ahí arriba…
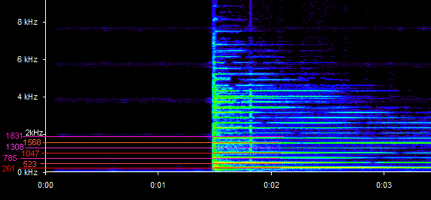
¿Es casualidad que coincidan con las líneas más largas e intensas del espectro? No, efectivamente no: estas líneas que aparecen claramente respecto a las demás son los armónicos de la nota del piano. Si miráis la tabla anterior, además, podréis comprobar que que el número 523 Hz ya aparecía antes, y es la nota Do 5. Pero no solo ésta: mirando una tabla completa, resulta que todas las frecuencias corresponden a una nota. Es más, de la siete primeras, cinco de ellas son notas Do o Sol en diferentes alturas, es decir, siempre octavas y quintas, los intervalos favoritos de los griegos. Aunque luego deja de haber octavas y quintas, los armónicos más importantes siempre forman estos invervalos.
Las frecuencias de los armónicos, el espectro, la elección de 5ª por los griegos como intervalo fundamental, todo aparece relacionado, y una y otra vez a lo largo de esta historia. A mí, que todo esto que se lleva haciendo desde la Antigua Grecia coincida con una precisión tan impresionante incluso en aparatos de medida modernos, realmente me fascina. Espero que hayáis disfrutado del artículo y veáis la música de una forma ligeramente distinta a partir de ahora.
Referencias
Para aprender más sobre el tema, se puede consultar en las siguientes fuentas:
- Burbano de Ercilla, S. Física General. Contiene un capítulo sobre Acústica dedicado fundamentalmente a la vibración de la cuerda y al método de las fracciones.
- Zamacois, J. Teoría de la Música. Uno de los manuales de referencia sobre teoría de la música. Incluye conceptos básicos sobre el sonido, su propagación, y la vibración tanto en cuerdas como en tubos. Además profundiza bastante en los sistemas de afinación y la comparación entre ellos.
