La saga de los penes I: Demostraciones del Teorema de Pitágoras usando pollas

Saga de los penes. Primer artículo

Saga de los penes. Segundo artículo

Texto escrito por Daniel Martínez y Fernando Cervera

ULÛM se suma a la iniciativa de Naukas conocida como #LunesPollas, en la cual, utilizando como excusa el instrumento viril, haremos un post de divulgación científica sobre el Teorema de Pitágoras [1]. El lector podrá pensar que no hay necesidad de hacer algo tan soez, pero sencillamente creemos que es una buena forma de escribir de algo interesante haciendo gala de nuestro sentido del humor y nuestra crítica, sobre todo después de lo sucedido con el primer divulgador que tuvo la iniciativa, Arturo Quirantes [2]. Así que prepárense para aterrizar en el mundo apasionante de Pitágoras y las pollas.

Demostraciones del famoso Teorema de Pitágoras las hay de muchas formas y colores: negras, caucásicas, largas, cortas, reales, imaginarias, geométricas, activas, pasivas, etc. Por ello hemos querido acercar a nuestros lectores algunas de ellas para que se introduzcan en el tema y puedan saborear en toda su forma y extensión estas maravillas del conocimiento humano.

Se estima que el Teorema de Pitágoras es uno de los que cuenta con más demostraciones. De hecho existe un texto muy interesante escrito por el matemático Elisha Scott Loomis, el cual describió 367 formas diferentes de llegar a la fórmula correcta en su libro The Pythagorean Proposition [3].

Podréis pensar que no existe una necesitad imperiosa de acumular tantas demostraciones, pero muchos autores consideran que en este caso es diferente porque en la Edad Media se exigía una nueva demostración del teorema para alcanzar el grado de Magíster matheseos. Esto habría ocasionado la aparición de muchas demostraciones independientes, aunque también es cierto de muchas de las que se pueden encontrar no tienen nada que ver con este hecho.

Una de las primeras demostraciones que queremos enseñaros es la siguiente: imaginemos que cogemos el pene de un senegalés y el pene de un murciano y los atamos desde su base con una cuerda, formando cuatro triángulos tal que las longitudes de sus catetos mayores y menores a y b respectivamente sean como los marcados en el primer dibujo. Los tenemos representados aquí:

Ahora disponemos los triángulos formados por los penes anteriores de la siguiente forma, para que se genere un cuadrado como el siguiente:

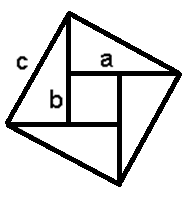Bien, recordemos que cada uno de los triángulos tiene un área igual a ab/2, y que por tanto, los cuatro triángulos tienen un área total de 2ab. También, si nos fijamos, tenemos un agujero cuadrado en el centro cuyos lados miden (a – b) cada uno. Entonces, teniendo estos datos, podemos formar la siguiente expresión y resolverla de forma sencilla:

c² = (a – b)² + 2ab = a² -2ab +b² + 2ab = a² + b²

¡Y así el teorema queda demostrado!

Otra de las demostraciones del teorema es la siguiente. En este caso se usan los principios de la geometría más que los del álgebra. Imaginemos que tenemos un triángulo rectángulo, formado por dos pollas de diferente tamaño atadas con un hilo desde su base, y con los vértices nombrados A (intersección de ambos miembros), B (base del pene asiático) y C (base del pene senegalés). Ahora, simplemente tenemos que establecer la altura del triángulo desde el vértice A (donde convergen los penes) al punto D. Se muestra en la siguiente imagen:

Ahora notad lo siguiente. Los triángulos ABC, DBA y DAC son similares pero diferentes en ratio, lo que nos lleva a las siguientes expresiones:

AB/BC = DB/AB; y AC/BC = DC/AC.

Si lo escribimos de otra forma, obtenemos: AB x AB = BD x BC; y AC x AC = DC x BC

Sumando ambas expresiones obtenemos:

AB x AB + AC x  AC =  BD x BC + DC x BC = (BD + DC) x BC = BC x BC

¡Y otra vez queda demostrado!

La última de estas demostraciones corresponde a un hombre que, en el siglo noveno después de Cristo, trabajó en una cuestión astronómica muy discutida en aquel entonces: la determinación numérica del movimiento de translación de la tierra. Thabit ibn Qurrá fue un matemático y astrónomo nacido en la actual Turquía, y sin ir más lejos llegó a ser uno de los investigadores de la famosa Casa de la Sabiduría de Bagdad. Los datos que obtuvo en cuanto a la translación terrestre fueron de tal exactitud que el mismo Copérnico alabó su trabajo siglos más tarde, ya que sorprendentemente Thabit calculó que la longitud del año era de 365 días, 6 horas, 9 minutos y 12 segundos. Es decir, solo cometió un error de 2 segundos en sus cálculos.

Por otro lado, su dominio de otros idiomas (árabe, griego y sirio) permitió que se convirtiera en uno de los primeros traductores de la casa de la sabiduría, y muchos textos como los Elementos de Euclides, algunas obras de Arquímedes, algunas partes de las Cónicas de Apolonio y el Almagesto de Tolomeo, fueron traducidas y conservadas hasta nuestros días gracias a este matemático. De hecho él fue el fundador de la escuela de traductores de Bagdad, de la cual salieron muchos textos que Europa, cuando llegó su oportuno renacimiento, utilizó para sembrar las semillas de la ciencia moderna. Thabit inb Qurra también aplicó la obra de Arquímedes sobre la cuadratura de la parábola para determinar áreas de figuras curvas, y que ese hecho ha sido descrito por muchos matemáticos como la aproximaciones más certera al uso del cálculo integral con esa finalidad.

La demostración que ofreció Thabit se encuentra en una carta que le respondió a un amigo que, conociendo la demostración de teorema para un triángulo rectángulo isósceles, le solicitaba la explicación del caso general para todos los triángulos. Thabit recurrió al método de reducción y composición, que consiste en reducir a triángulos y luego recomponerlos por yuxtaposición. De este modo Thabit mandó dos soluciones a su amigo, de las cuales solo representaremos una:

Sea el triángulo rectángulo ABC. Si a la figura ABCDEF se le sustraen los triángulos ABC y CDE iguales al dado, resulta el cuadrado ACEF construido sobre la hipotenusa AC, mientras que sustrayendo los triángulos AHF y FGE, resulta la figura formada por los cuadrados ABIH, GIDE, construidos sobre los catetos AB, BC.

Esta última demostración geométrica es complicada de comprender pero en muchos colegios se utiliza para explicar el Teorema de Pitágoras, ya que si se recortan los triángulos y se superponen de una manera determinada queda muy claro. Nos obstante no nos ha parecido ético cortar el pene a estas personas para hacer una demostración más efectiva, así que hemos decidido dejarlo así. [4]

Para terminar con este artículo sobre penes y teoremas queremos invitaros desde ULÛM a que profundicéis más en ambas temáticas, ya que tratadas de la forma correcta pueden dar historias interesantes. Así que no lo olvidéis: haced vuestra vida más intensa con un montón de buenos rabos y teoremas.

 Referencias:

[1] Enlace a Naukas

[2] Enlace a Naukas II

[3] http://Enlace 3

[4] Enlace 4